Batch 3 - Class 113 - Pizza Slicing, Magic Triangles
Pre-Class Problem:
- Six other people were in a mansion when Mr. Edwards was murdered in the attic, but each has an alibi backed up by another person. Ms. Abbott says that she saw Vicar Carter reading in the study at the time. Mrs. Blyth says she saw Ms. Doyle exit the mansion for a walk. Vicar Carter says he saw Mr. Gibson walking the grounds as he looked out the window. Ms. Doyle says she saw Mrs. Foseberry in the garden. Mr. Gibson says he saw Ms. Abbott dusting the hallway. Mrs. Foseberry says she saw Mrs. Blyth in the sitting room through the window. Each person confirms that they were doing what they were observed to be doing. If at least one of the six were involved in the murder, what is the minimum number of them who are lying?
- Answer: Two
Attendance: Smiti, Muskaan, Anisha, Arushi, Tishyaa, Nandini, Aneyaa, Arnav, Anishka, Ishaan, Kabir, Manya, Diya, Arnav, Zorawar
Class Notes:
Slicing a Laaarge Pizza
If you had a very large (infinite) pizza, and you were allowed to make 10 straight cuts, what is the maximum number of slices you could divide it into? Note that the slices do not have to be equal.
- Explore with kids whether the number of regions always has to be the same, given a number of cuts
- For example, with 2 cuts, how many regions can we get? 3 or 4 - we lose a region if we have parallel lines
- With 3 cuts, how many can we get? 4, 6 or 7 - we lose a region if more than 2 cuts pass through the same point
- What do we do to maximize the number of regions
- Answer: Ensure every line cuts every other line, and no three line pass through the same point
- So not, lets try to solve smaller problems
- What the maximum number of slices we can get with 2 cuts - Answer: 4
- What the maximum number of slices we can get with 3 cuts - Answer: 7
- What the maximum number of slices we can get with 4 cuts - Answer: 11
.png)
- What is the pattern above?
- One way to look at the pattern is that amongst successive numbers, the successive difference goes up by 1. Can you explain this?Answer: If you already have 4 lines and you are drawing the fifth line, then this fifth line will intersect each other line once, and for each intersection, it will create a new region once
- Another way to look at it is that f(n+1) = 2.f(n) - nC2. Can you explain this?Answer: If we were able to divide each region, we would have 2.f(n). But for any pair of lines, a new line can only cut across three out of four regions formed by those two lines. So we lose one region for each pair of lines
- So what is f(10)? f(20)?
- Can you find a simple formula for f(n)?
- Answer: Sum of first n numbers + 1
- Can you find an intuitive logic for this simple formula?
Magic Triangle
We see a triangle with three sides and six slots below. In how many ways can we put numbers 1,2,3,4,5,6 in these slots, so that sum of each side is the same? Two solutions are regarded the same if they are mere rotations or flips of other solutions.
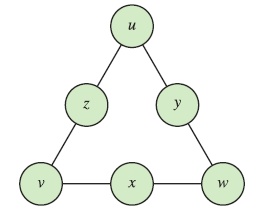
Instructor Notes: Let kids try to come up with different solutions for a while. See if they come up with all the solutions. If they claim they have found all, then ask them to prove it.
Solution:
If C is sum of corner slots, and M is sum of middle squares, then C+M=21
Also, if sum of each side is S, then 3S = 2C+M (In the three sides, each corner gets counted twice, and each middle once)
Hence C = 3(S-7) and M = 3(14-S) . Note that both C and M are multiples of 3
Also, since C and M are both sum of three numbers, they can only be between 6 and 15.
Lets tabulate all the possibilities:
Possibility 1 | Possibility 2 | Possibility 3 | Possibility 4 | |
C | 6 | 9 | 12 | 15 |
M | 15 | 12 | 9 | 6 |
S | 9 | 10 | 11 | 12 |
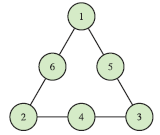 | 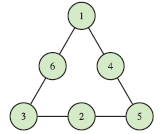 | 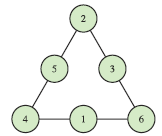 | 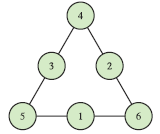 |
Any other interesting patterns you can observe?
- Whats the relationship between pairs of corner and opposite middle in any given diagram?
- Whats the relationship between solutions 1 and 4? and between 2 and 3?
Homework
- Can you solve the above magic triangle for 9 digits instead of 6?
.png)
- Solution: There is one solution for each S value between 17 and 23, corresponding to C values between 6 and 24 - i.e there are 7 solutions. Check if number of solutions for 1..12 could be 10.
References: